Additiva si, additiva no
 Come è noto la produzione additiva presenta vantaggi e svantaggi. I primi sono sostanzialmente dovuti al fatto che con queste tecniche è possibile realizzare componenti molto complessi, a volte impossibili da realizzare con le tecniche tradizionali. I principali problemi sono ancora legati alla relativa lentezza del processo di fabbricazione, alle finiture superficiali e alle tensioni residue del processo. Per massimizzare i vantaggi di queste tecniche di produzione occorre fare due considerazioni. La prima è che non tutti i componenti sono adatti ad essere realizzati mediante produzione additiva (o meglio non sono economicamente vantaggiosi), infatti componenti massivi, in cui sono presenti ampi volumi in cui il materiale è compatto, non sono economicamente vantaggiosi se realizzati con la produzione additiva. Invece beneficiano molto di queste tecniche strutture che potremmo definire “a bassa densità”, ossia componenti complessi in cui il volume “vuoto” rispetto al volume totale è molto elevato. La seconda considerazione è legata alla progettazione dei componenti, infatti la produzione additiva, consentendo di depositare il materiale solo dove serve è il metodo di produzione ideale per consentire l’ottimizzazione topologia dei componenti, riducendo al minimo il peso pur preservando determinate specifiche di resistenza e rigidezza.
Come è noto la produzione additiva presenta vantaggi e svantaggi. I primi sono sostanzialmente dovuti al fatto che con queste tecniche è possibile realizzare componenti molto complessi, a volte impossibili da realizzare con le tecniche tradizionali. I principali problemi sono ancora legati alla relativa lentezza del processo di fabbricazione, alle finiture superficiali e alle tensioni residue del processo. Per massimizzare i vantaggi di queste tecniche di produzione occorre fare due considerazioni. La prima è che non tutti i componenti sono adatti ad essere realizzati mediante produzione additiva (o meglio non sono economicamente vantaggiosi), infatti componenti massivi, in cui sono presenti ampi volumi in cui il materiale è compatto, non sono economicamente vantaggiosi se realizzati con la produzione additiva. Invece beneficiano molto di queste tecniche strutture che potremmo definire “a bassa densità”, ossia componenti complessi in cui il volume “vuoto” rispetto al volume totale è molto elevato. La seconda considerazione è legata alla progettazione dei componenti, infatti la produzione additiva, consentendo di depositare il materiale solo dove serve è il metodo di produzione ideale per consentire l’ottimizzazione topologia dei componenti, riducendo al minimo il peso pur preservando determinate specifiche di resistenza e rigidezza.
Le strutture reticolari
Le tecnologie di produzione additiva, a differenza delle tecnologie di fabbricazione tradizionali, consentono di realizzare strutture reticolari (lattice) e alveolari composte da un insieme di elementi bidimensionali (travi) opportunamente orientati nello spazio. La disposizione e la densità di questo elementi può essere calibrata in modo tale da conferire al componente le proprietà meccaniche desiderate. La progettazione di questo tipo di strutture tuttavia non è attualmente supportata da strumenti di simulazione idonei a sostenere la complessità geometrica che le contraddistingue. Altro interessante ambito di applicazione delle tecnologie additive sono le strutture biomimetiche, con le quali il progettista tenta di rispondere ad un determinato requisito strutturale ispirandosi a strutture di origine naturale, la cui forma e distribuzione del materiale è frutto della millenaria evoluzione degli esseri viventi. Esempio in questo senso sono componenti a densità variabile come le ossa o il corallo, condotti di lubrificazione o raffreddamento distribuiti in modo capillare come nelle strutture vegetali. Negli ultimi anni, con il perfezionamento delle tecniche di produzione additiva e i maggiori investimenti per la ricerca in questo campo, si è potuto appurare quanto i risultati ottenibili tramite processi di ottimizzazione strutturale siano diventati facilmente realizzabili. L’ottimizzazione del design di un oggetto può condurre a notevoli miglioramenti nella forma e nelle caratteristiche finali dello stesso.
Tre vie per ottimizzare
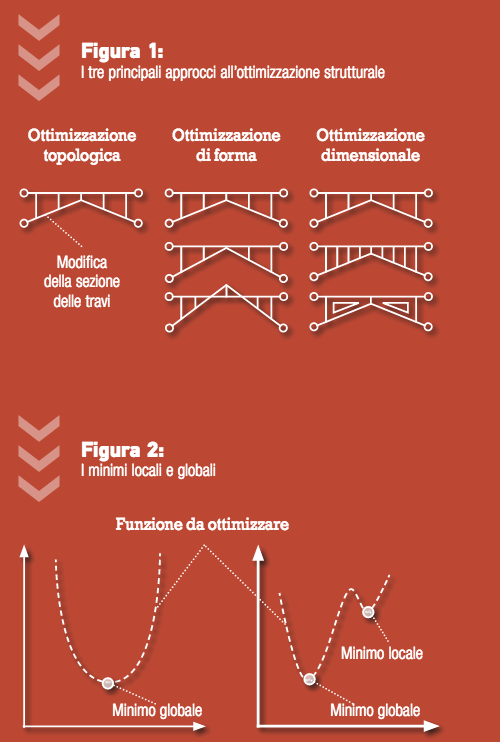
Ottimizzazione topologica: non vi è una dimensione o una forma prestabilite. Vi è uno spazio di design all’interno del quale deve essere ottimizzata la distribuzione del materiale affinchè sia garantita la resistenza ai carichi imposti. Uno tra i più diffusi metodi di ottimizzazione topologica è il metodo SIMP (solid isotropic material with penalisation) che stabilisce una relazione tra la rigidezza degli elementi di una struttura e la loro densità. Per chiarire la distinzione fra questi tre approcci all’ottimizzazione strutturale, nella Figura 1 sono mostrate tre diverse geometrie che differiscono tra loro per la distribuzione di materiale ma sono tutte in grado di sopportare il carico imposto.
Cosa fa il software
La corsa agli algoritmi
• metodo “simulated annealing”: è una semplice tecnica utilizzabile per trovare il minimo globale in problemi aventi più minimi locali (Figura 2). L’idea è di generare un insieme casuale di punti che si trovano nelle vicinanze dell’ottimo ipotetico e calcolare le soluzioni del problema in quei punti. Se il valore della funzione obiettivo ricalcolata nei nuovi punti offre una migliore ottimizzazione, il nuovo punto è considerato come punto di ottimo. La sostituzione del vecchio ottimo con il nuovo si basa su un approccio probabilistico.
*Andrea Mura è Assegnista di Ricerca presso il Dipartimento di Ingegneria Meccanica e Aerospaziale del Politecnico di Torino. È membro del comitato tecnico della rivista Organi di Trasmissione di Tecniche Nuove e del comitato editoriale delle riviste American Journal of Science and Technology e Journal of Mechanics Engineering and Automation. Fa ricerca su trasmissioni meccaniche e progettazione di macchine.